L’epoca in cui Johannes Keplero operò fu segnata da rivoluzioni concettuali e metodologiche che stravolsero il paradigma astronomico consolidato. Partendo dai dati osservativi del celebre astronomo danese Tycho Brahe, Keplero reinterpretò il moto planetario. Una delle intuizioni più rivoluzionarie fu abbandonare il modello delle orbite perfettamente circolari, accolto per secoli, per abbracciare la bellezza matematica delle ellissi. Questa svolta non solo demolì teorie millenarie, ma pose le fondamenta per la meccanica celeste moderna, aprendo la via ai successivi lavori di Newton e ad un approfondito studio sulla gravitazione universale.
La prima legge
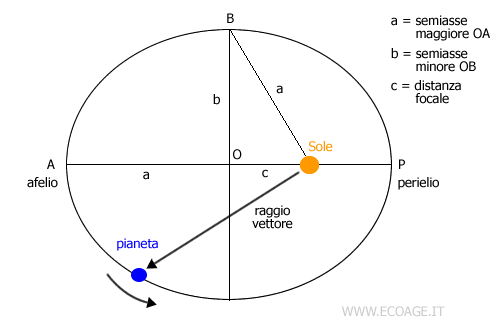
Enunciato: Tutti i pianeti si muovono attorno al Sole lungo orbite ellittiche, dove il Sole stesso occupa uno dei fuochi dell’ellisse.
Eliminando l’idea delle orbite circolari, Keplero dimostrò che la vera natura del moto planetario è descritta da un’ellisse, una forma geometrica caratterizzata da 2 fuochi, con il Sole posizionato in uno di essi. In un sistema di coordinate polari, l’equazione dell’ellisse può essere scritta come:
r = p⁄(1 + e · cosθ)
dove:
r rappresenta la distanza dal fuoco,
p è il semilatus rectum,
e è l’eccentricità, misura di quanto l’ellisse sia “schiacciata”, e
θ l’angolo polare.
Questa formulazione non solo rende esplicito il cambiamento di distanza tra il pianeta e il Sole, variabile lungo l’orbita, ma spiega anche le variazioni dinamiche osservate nei moti celesti. L’evidenza empírica derivata dalle osservazioni meticolose di Tycho Brahe fornì a Keplero i dati necessari per confermare con estrema precisione che nessun pianeta segue una traiettoria perfettamente circolare.
La seconda legge
Enunciato: Un segmento di linea che unisce un pianeta al Sole spazza aree uguali in intervalli di tempo uguali.
Questa legge, nota come “Legge delle aree”, rivela che la velocità di un pianeta non è costante lungo la sua orbita: esso si muove più velocemente in prossimità del perielio (il punto più vicino al Sole) e più lentamente nell’afelio (il punto più distante). La ragione risiede nella conservazione del momento angolare, che implica che l’areal velocity, ossia la velocità con cui l’area viene spazzata, rimane costante. Un’espressione matematica che lo sintetizza è:
(dA/dt) = L⁄(2m)
dove:
dA/dt rappresenta la velocità areale,
L è il momento angolare del pianeta, e
m la sua massa.
Questa relazione esplica che, pur variando localmente la velocità lineare, la “spinta” complessiva (espressa dal momento angolare) è preservata lungo l’intera orbita. I dati combinati di osservazioni accurate e la successiva validazione teorica hanno confermato l’infallibilità di questo principio, dimostrando come il moto planetario rispetti una simmetria profonda e universale.
La terza legge
Enunciato: Il quadrato del periodo orbitale di un pianeta è proporzionale al cubo del semiasse maggiore della sua orbita.
Conosciuta anche come “Legge delle armonie”, la terza legge di Keplero stabilisce una relazione matematica tra la durata dell’orbita di un pianeta (il suo periodo, T) e la dimensione dell’orbita stessa (espressa dal semiasse maggiore, a). Formalmente:
T² ∝ a³
In unità astronomiche (dove il tempo è misurato in anni terrestri e la distanza in unità astronomiche: AU), la costante di proporzionalità si semplifica a 1, cioè:
T² = a³
Questa relazione, d’effetto e sorprendentemente semplice, sottolinea come il moto dei pianeti segua un’armonia matematica universale, in cui i pianeti più distanti dal Sole impiegano tempi significativamente maggiori per completare la loro rivoluzione. Tale correlazione non solo ha permesso di prevedere con incredibile precisione le orbite planetarie ma ha fornito anche un ponte fondamentale per la successiva formulazione della legge di gravitazione universale di Newton.
Quali riflessioni suscita in te l’idea che l’universo sia governato da leggi così eleganti e precise? In che modo credi che questa visione possa influenzare il nostro modo di comprendere il cosmo e il nostro posto al suo interno? Scrivicelo nei commenti, oppure esplora altri articoli su AstroCuriosità!
Fonti: NASA, Britannica, ScienceFacts











